Element distinctness problem
In computational complexity theory, the element distinctness problem or element uniqueness problem is the problem of determining whether all the elements of a list are distinct.
It is a well studied problem in many different models of computation. The problem may be solved by sorting the list and then checking if there are any consecutive equal elements; it may also be solved in linear expected time by a randomized algorithm that inserts each item into a hash table and compares only those elements that are placed in the same hash table cell.[1]
It is known that the problem's time complexity is Θ(n log n), i.e., both the upper and lower bounds on its time complexity are of order of the linearithmic function in the algebraic decision tree model of computation,[2] a model of computation in which the elements may not be used to index the computer's memory (as in the hash table solution) but may only be accessed by computing and comparing simple algebraic functions of their values. In other words, an asymptotically optimal algorithm of linearithmic time complexity is known for this model. The algebraic computation tree model basically means that the allowable algorithms are only the ones that can perform polynomial operations of bounded degree on the input data and comparisons of the results of these computations.
The same lower bound was later proved for the randomized algebraic decision tree model.[3]
It is also known that quantum algorithms can solve this problem faster in 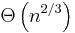 queries. The optimal algorithm is by Andris Ambainis,[4] and the lower bound is due to Scott Aaronson and Yaoyun Shi.[5]
queries. The optimal algorithm is by Andris Ambainis,[4] and the lower bound is due to Scott Aaronson and Yaoyun Shi.[5]
Several lower bounds in computational complexity are proved by reducing the element distinctness problem to the problem in question, i.e., by demonstrating that the solution of the element uniqueness problem may be quickly found after solving the problem in question.
Restrictions
Decision tree models are inapplicable for determining lower bounds for algorithmic problems for objects that have some a priori properties which can be exploited in construction of algorithms. For example, if it is known that the n objects are integer numbers from the range [1..n], then the element uniqueness problem may be solved in O(n) time by a modification of bucket sort.
Generalization: Finding repeated elements
Elements that occur more than n/k times in a multiset of size n may be found in time O(n log k). The element distinctness problem is a special case of k=n. This algorithm is optimal under the decision tree model of computation.[6]
The algorithm is a generalization of the one for a special case of k=2, which had a rather convoluted history of publication.[7]
The above algorithms rely only on the test of identity of the elements. If sorting is allowed, previously known order statistics finding algorithms may be exploited. For example, for k=2, a median may be found first in linear time, and then it may be easily tested whether there are more than n/2 median elements. However the above algorithms require fewer comparisons than the order statistics algorithms.[7]
References
- ^ Gil, J.; Meyer auf der Heide, F.; Wigderson, A. (1990), "Not all keys can be hashed in constant time", Proc. 22nd ACM Symposium on Theory of Computing, pp. 244–253, doi:10.1145/100216.100247.
- ^ Ben-Or, Michael (1983), "Lower bounds for algebraic computation trees", Proc. 15th ACM Symposium on Theory of Computing, pp. 80–86, doi:10.1145/800061.808735.
- ^ Grigoriev, Dima; Karpinski, Marek; Heide, Friedhelm Meyer; Smolensky, Roman (1996), "A lower bound for randomized algebraic decision trees", Computational Complexity 6 (4): 357, doi:10.1007/BF01270387.
- ^ Ambainis, Andris (2007), "Quantum walk algorithm for element distinctness", SIAM Journal on Computing 37 (1): 210–239, arXiv:quant-ph/0311001, doi:10.1137/S0097539705447311.
- ^ Aaronson, S.; Shi, Y. (2004), "Quantum lower bounds for the collision and the element distinctness problems", Journal of the ACM 51 (4): 595–605, doi:10.1145/1008731.1008735, ISSN 0004-5411.
- ^ Misra, J.; Gries, D. (1982), "Finding repeated elements", Science of Computer Programming 2: 143–152.
- ^ a b Boyer, R. S.; Moore, J S. (1991), "MJRTY - A Fast Majority Vote Algorithm", in Boyer, R. S., Automated Reasoning: Essays in Honor of Woody Bledsoe, Automated Reasoning Series, Dordrecht, The Netherlands: Kluwer Academic Publishers, pp. 105–117.